Neural Unsigned Distance Fields for Implicit Function Learning

Abstract

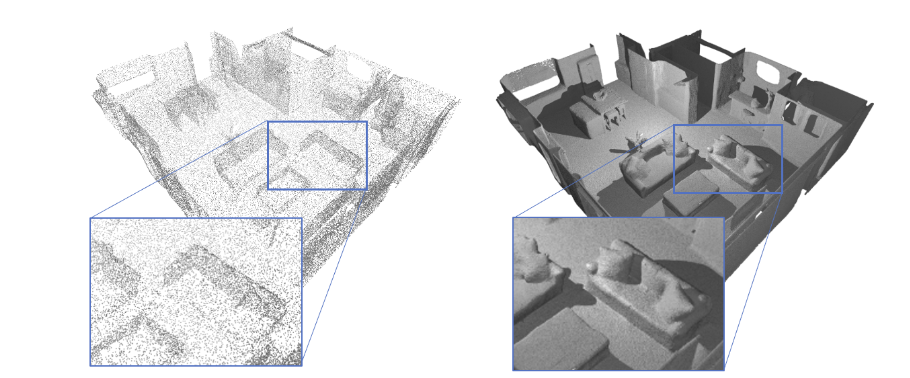
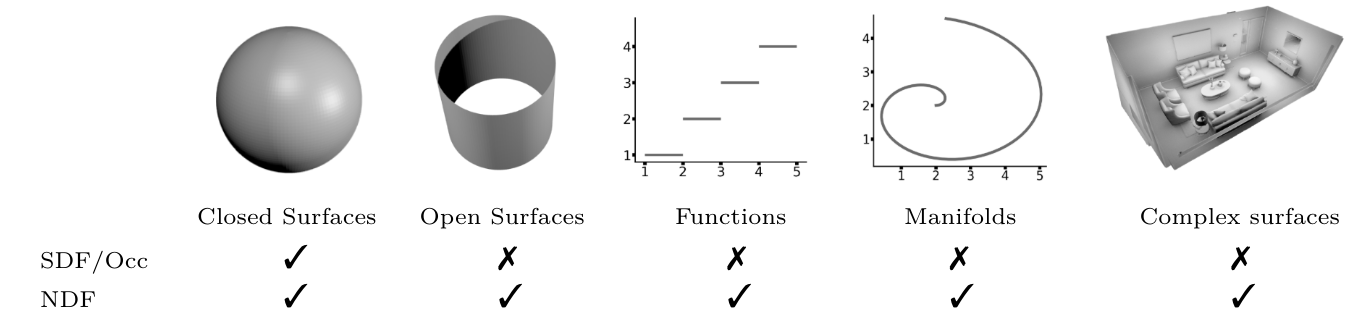
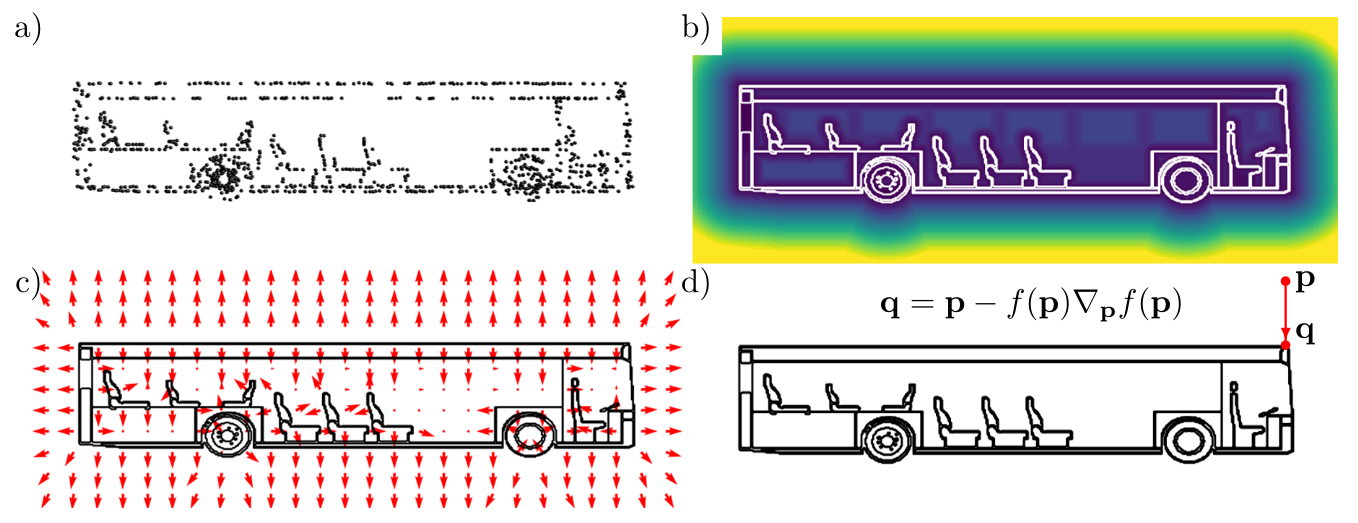
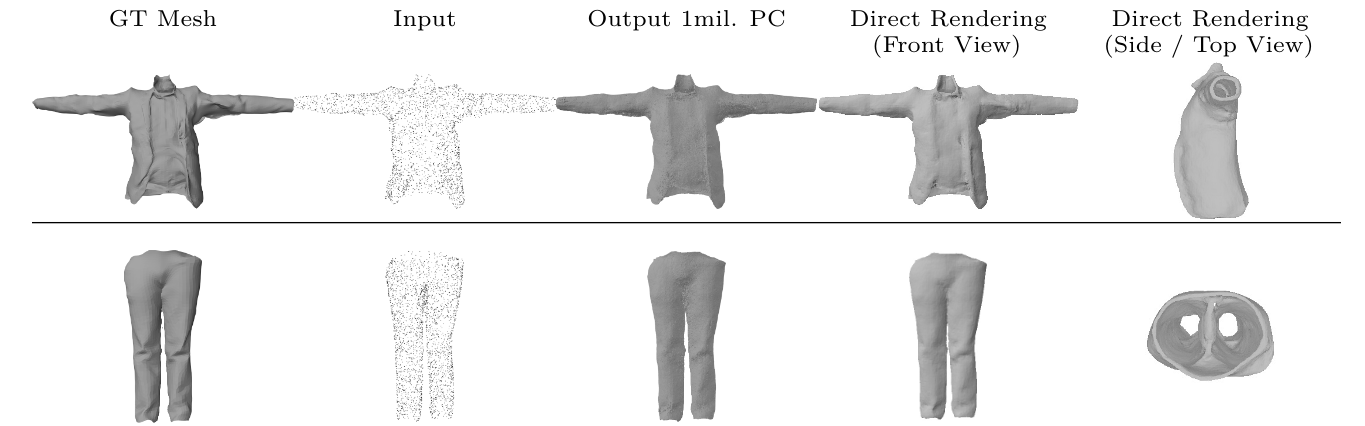
In this work we target a learnable output representation that allows continuous, high resolution outputs of arbitrary shape. Recent works represent 3D surfaces implicitly with a Neural Network, thereby breaking previous barriers in resolution, and ability to represent diverse topologies. However, neural implicit representations are limited to closed surfaces, which divide the space into inside and outside. Many real world objects such as walls of a scene scanned by a sensor, clothing, or a car with inner structures are not closed. This constitutes a significant barrier, in terms of data pre-processing (objects need to be artificially closed creating artifacts), and the ability to output open surfaces. In this work, we propose Neural Distance Fields (NDF), a neural network based model which predicts the unsigned distance field for arbitrary 3D shapes given sparse point clouds. NDF retain the good properties of recent implicit learning methods, but do not require pre-processing, and significantly broaden the class of representable shapes. NDF represent surfaces at high resolutions as prior implicit models, but do not require closed surface data, and significantly broaden the class of representable shapes in the output. Since classical methods (such as marching cubes) for mesh reconstruction and rendering assume a signed distance field, learning NDF poses additional challenges. To reconstruct a dense point-cloud, we simply sample points in space and query the distance and gradient values analytically using NDF; then we project points to the surface by shifting them along the gradient d distance units. NDF allow to extract the surface as very dense point clouds and as meshes. We also show that NDF allow for surface normal calculation and can be rendered using a slight modification of sphere tracing and can be used for multimodal regression (multiple outputs for one input) with techniques that have been exclusively used for rendering in graphics. We find NDF can be used for multi-target regression (multiple outputs for one input) with techniques that have been exclusively used for rendering in graphics. Experiments on ShapeNet show that NDF, while simple, is the state-of-the art, and allows to reconstruct shapes with inner structures, such as the chairs inside a bus. Notably, we show that NDF are not restricted to 3D shapes, and can approximate more general open surfaces such as curves, manifolds, and functions.